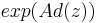Levi decomposition
In Lie theory and representation theory, the Levi decomposition, conjectured by Killing and Cartan and proved by Eugenio Elia Levi (1905), states that any finite dimensional real Lie algebra g is the semidirect product of a solvable ideal and a semisimple subalgebra.
Contents |
Formal statement
One is its radical, a maximal solvable ideal, and the other is a semisimple subalgebra, called a Levi subalgebra. Levi decomposition implies that any finite dimensional Lie algebra is a semidirect product of a solvable Lie algebra and a semisimple Lie algebra.
When viewed as a factor-algebra of g, this semisimple Lie algebra is also called the Levi factor of g. Moreover, Malcev (1942) showed that any two Levi subalgebras are conjugate by an (inner) automorphism of the form
where z is in the nilradical (Levi–Malcev theorem).
Application
To a certain extent, the decomposition can be used to reduce problems about finite dimensional Lie algebras and Lie groups to separate problems about Lie algebras in these two special classes, solvable and semisimple.
Extensions of the results
In representation theory, Levi decomposition of parabolic subgroups of a reductive group is needed to construct a large family of the so-called parabolically induced representations. The Langlands decomposition is a slight refinement of the Levi decomposition for parabolic subgroups used in this context.
Analogous statements hold for simply connected Lie groups, and, as shown by George Mostow, for algebraic Lie algebras and simply connected algebraic groups over a field of characteristic zero.
There is no analogue of the Levi decomposition for most infinite-dimensional Lie algebras; for example affine Lie algebras have a radical consisting of their center, but cannot be written as a semidirect product of the center and another Lie algebra. The Levi decomposition also fails for finite dimensional algebras over fields of positive characteristic.
See also
References
- Jacobson, Lie algebras
- Levi, Eugenio Elia (1905), "Sulla struttura dei gruppi finiti e continui" (in Italian), Atti della Reale Accademia delle Scienze di Torino. XL: 551–565, JFM 36.0217.02, archived from the original on March 05, 2009, http://www.archive.org/stream/attidellarealeac40real#page/550/mode/2up Reprinted in: Opere Vol. 1, Edizione Cremonese, Rome (1959), p. 101.
- Maltsev, Anatoly I. (1942), "On the representation of an algebra as a direct sum of the radical and a semi-simple subalgebra", C. R. (Doklady) Acad. Sci. URSS (N.S.) 36: 42–45, MR0007397, Zbl 0060.08004.
External links
- A.I. Shtern (2001), "Levi-Mal'tsev decomposition", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=l/l058250